Data Structures in Clojure: Hash Tables

Where We Left Off

Last time we looked at linked lists. Specifically, we explored how one might go about implementing a mutable, singly-linked list. We touched briefly on reasons for doing this and it is important to point out that generally Clojure prefers immutable variants of these data structures. However there are legitimate scenarios where an algorithm is both simpler and faster when mutation is utilized. In practice, you will use Clojure’s data structures when writing Clojure programs, but for the purpose of better understanding Clojure and data structures this series will take a different approach. It aims to take a closer look at definterface and deftype, specifically, which often seem neglected in other texts.

Here we will build on our prior work with linked lists and construct a data structure that satisfies the abstract data type known as an associative array or dictionary. To do this, we will implement a hash table.

Our hash table implementation will address issues such as hash collisions and runtime performance guarantees. We will iterate on our implementation, addressing each of these in turn. Finally we will briefly discuss type hints and their importance with regard to performance. While the implementation we end up with will not be a substitute for Java or Clojure’s implementation, it will be a solid illustration of the principles behind their implementation– immutability notwithstanding.

Hash Tables

A hash table or hash map is an implementation of an associative array, an abstract data type. The primary function of an associative array is to allow for the insertion, lookup, and deletion of values by keys. For example, if we wanted to store a value "bar" we could assign it to the key "foo". Later, using this key "foo", we could retrieve the value "bar" from the hash table. Thus we establish an association between the key "foo" and the value "bar" maintained by the data structure.

Associative mappings like the above are a common data structure in many languages. For instance, Python programmers will be familiar with the language’s dictionary type. Similarly, Clojure programmers will no doubt have made extensive use of hash maps. Our hash table will work much like these, with the important distinction, as compared to Clojure, that our associative array will be mutable.

Performance Characteristics

An important property of a hash table is the performance guarantees it makes. Hash tables provide insertion, lookup, and deletion in O(1) time, on average. While linked lists provide good access to the first element of the list, O(1), finding an element in the list may be considerably more expensive, O(n), because we may have to traverse the entire list.

In practice, cache locality, the hashing function used to discover indexes, and collision handling schemes such as separate chaining and open addressing will affect actual performance; nevertheless we should still beat our linked list in terms of performance.

Implementation Details

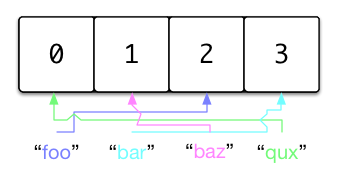
Our hash table will be backed by an array of “buckets”. This is where all our data will live and is the fundamental piece of our data structure. We can think of the hash table as being an indexer that wraps this array. The indexes will in fact be Nodes. If we recall our previous look at linked lists, we will use these nodes as a starting point. This structuring is known as separate chaining.

To illustrate how this will work, imagine we have a simple array. When we give our hash table a key and a value, they will be placed in an index on the underlying buckets array. We will cover this in more detail in a bit. For now, just understand that our data structure will handle where in the array that key-value pair is placed, i.e. it will do the indexing for us.

Simple Array

In order to make certain operations easier, we will also modify our original Node class such that it has three fields: key, value, and next. While we could continue to use our previous implementation without modification, this will make setting and getting the keys and values simpler.

Basic Implementation

HashTable Class

Building upon our previous linked list implementation, we will introduce a new type called HashTable. Much like the Node class, it will use an interface to define a set of functions that can be used with the class. Our initial code will look like this:

(definterface INode
  (getKey [])
  (setKey [k])
  (getVal [])
  (setVal [v])
  (getNext [])
  (setNext [n]))

(deftype Node
  [^:volatile-mutable key
   ^:volatile-mutable val
   ^:volatile-mutable next]
  INode
  (getKey [this] key)
  (setKey [this k] (set! key k))
  (getVal [this] val)
  (setVal [this v] (set! val v))
  (getNext [this] next)
  (setNext [this n] (set! next n)))

(definterface IHashTable
  (insert [k v]))

(deftype HashTable
  [buckets size]
  IHashTable
  (insert [this k v]))

Note that our linked list implementation has diverged from our original, as promised. Also for the time being we have not properly implemented our hash table type and its insert method. We will cover this shortly, but before we dive in we should explore how precisely a key-value pair is associated with the buckets array.

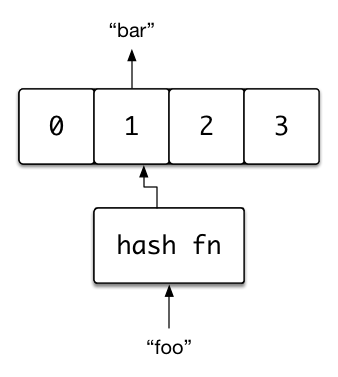
Our key-value pairs will live in nodes as part of a linked list. This will be important later when we talk about handling collisions. These nodes will be mapped onto an index in the buckets array. To find a node’s index in the array, we take its key and hash it; this is the “hash” of “hash table”. To ensure the hash corresponds to a valid index, we need to take the modulus of the hash and the number of buckets. This ensures that we always end up with a valid index.

Hash Mapped Key-Values

Now with this in mind we should be able to implement our insertion method:

(definterface IHashTable
  (bucketIdx [k])
  (setBucket [k v])
  (insert [k v]))

(deftype HashTable
  [buckets size]
  IHashTable
  (bucketIdx [_ k] (mod (hash k) size))
  (setBucket [this k v] (aset buckets (.bucketIdx this k) v))
  (insert [this k v]
    (.setBucket this k (Node. k v nil))))

Note that aset is a special Clojure function for setting values on array indexes. Although Java arrays are uncommon in Clojure itself, in the interest of streamlining Java interop, methods such as aset, aget, and alength exist. We will use these for operations on the buckets array.

Okay. We now have a way to insert keys and values into the underlying buckets array. This could be used like this:

=> (def hash-table
     (let [size 4]
       (HashTable. (make-array INode size) size)))
#'user/hash-table
=> (.insert hash-table "foo" "bar")
#<Node user.Node@2753d864>

Here we have defined our hash table by passing it an array containing INodes of size size. We have also set the hash table’s size to size. Of course we have neglected to give ourselves a way to see what actually resides in the hash table. So before we go any further we will implement a lookup method:

(definterface IHashTable
  (bucketIdx [k])
  (getBucket [k])
  (setBucket [k v])
  (insert [k v])
  (lookup [k]))

(deftype HashTable
  [buckets size]
  IHashTable
  (bucketIdx [_ k] (mod (hash k) size))
  (getBucket [this k] (aget buckets (.bucketIdx this k)))
  (setBucket [this k v] (aset buckets (.bucketIdx this k) v))
  (insert [this k v]
    (.setBucket this k (Node. k v nil)))
  (lookup [this k]
    (when-let [node (.getBucket this k)]
      (.getVal node))))

Great! We should now be able to retrieve our key-value pairs:

=> (.lookup hash-table "foo")
"bar"

When we set out to create our hash table we specified a size of 4. Why is this important? Recall that in order to bound our hashes by the length of our buckets array we used the size value. This is all well and good until the underlying array fills up. What happens then?

Collisions

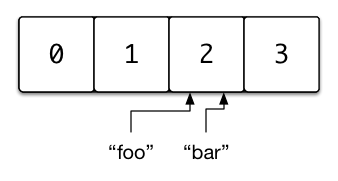
Keys Hashing to the Same Index

When two keys hash to the same index, they collide, this is a collision. It is a situation all hash tables have to handle in some way. For our implementation we will use a strategy known as separate chaining. Alternatively, we could have used open addressing. There are other variations based on separate chaining and open addressing but they are a bit beyond the scope of this post.

Right now, if two keys collide in our hash table, the node will be overwritten and the old key-value pair will be lost. This is obviously not desirable. But when we choose to use linked lists as the values of our buckets we were actually planning for such a situation already!

How do linked lists solve this problem? Well when we find ourselves with a collision we can simply tack a new node onto the bucket. Recall that linked lists can be prepended to cheaply. All we then need to do is handle cases where a bucket already contains a node by consing a new node onto that bucket. This also implies our lookup strategy should change slightly to account for this by walking the nodes of a given bucket.

Let us go ahead and make these changes now:

(definterface IHashTable
  (findNode [k])
  (insert [k v])
  (lookup [k]))

(deftype HashTable
  [buckets size]
  IHashTable
  ...

  (findNode [this k]
    (when-let [bucket (.getBucket this k)]
      (loop [node bucket prev nil]
        (if (or (nil? node) (= (.getKey node) k))
          (vector prev node)
          (recur (.getNext node) node)))))

  (insert [this k v]
    (let [[prev node] (.findNode this k)]
      (cond
        ;; 1. bucket contains a linked list but not our key,
        ;;    set the next node
        (and prev (nil? node)) (.setNext prev (Node. k v nil))

        ;; 2. bucket contains a linked list and our key, reset 
        ;;    value
        node (.setVal node v)

        ;; 3. bucket is empty, create a new node and set the 
        ;;    bucket
        :else (.setBucket this k (Node. k v nil)))))

  (lookup [this k]
    (let [[_ node] (.findNode this k)]
      (when node
        (.getVal node)))))

Now we have a way of handling hash collisions. Here we implemented our strategy of consing new nodes onto occupied buckets. To do this, we also added a helper method findNode, which takes a key and attempts to locate the key in the buckets array. If it does, it returns the node containing the key and the node directly before that node, if any. With the previous node and the node containing the key, we can then determine exactly which case we are dealing with in the scope of our insertion method:

If we have a previous node but not a node, then we know we have an occupied bucket but that our key does not already exist. In this case, we cons a new node onto the bucket.
We have a node. This means the key is already contained in the bucket’s linked list. Here all we want to do is update the value the node contains.
We know that the bucket is empty and therefore cannot contain the key. So we simply set the bucket with a new node containing our key and value and point to no next node.

Guaranteeing Runtime Complexity

With collisions out of the way, we are moving closer to a practical implementation of a hash table. But there remains a fairly important issue with our hash table as it stands. What happens if we create a hash table with a small size and set a number of keys on it?

=> (def hash-table
     (let [size 1]
       (HashTable. (make-array INode size) size)))
=> (.insert hash-table "foo" "bar")
=> (.insert hash-table "bar" "baz")
=> (.insert hash-table "baz" "qux")
=> (.lookup hash-table "foo")
"bar"

When our array’s length is 1, as in this example, we will have collisions with the insertion of every key-value. Of course this is handled by our updated implementation but it does not account for our performance promises. In the above situation we have to traverse the entire linked list to retrieve "bar", yielding O(n) time.

This is not desirable. So what would the ideal situation look like? To maximize efficiency in space and time, we would like each index in the buckets array to be filled and contain exactly one node. Such a scenario would be pretty much as good as it gets. In practice, we will not achieve this. But we can do better than what we have currently.

If we think about our buckets array we might notice that there is a relationship between its size and the efficiency with regard to the hash table methods. More precisely, if the buckets array is too small, we are forced to create deeper buckets and if it is too big, then we are wasting memory. Perhaps what we need is a heuristic for resizing our array?

Our goal here should be to keep the buckets array as full as possible while keeping the buckets as shallow as possible. Assume that we maintain a record of the number of occupied indexes in our buckets array. Upon insertion and deletion, we could then call a method that determines if we should resize it. This would operate by copying the old buckets and placing them into a new array of a larger or smaller size. We should also implement a method that determines what the new size should be.

Resizing the array will be an expensive operation so we should try to do it as infrequently as possible, while still fulfilling our original goal. Initially we will use a load factor of 70%. This means that when the underlying array is ~70% occupied, additional insertions will trigger a resize. In the case of downsizing we want to ensure that we do not scale down only to immediately scale back up, so we will only downsize when it would allow for a fairly empty array, e.g. ~30% occupied. Alternatively, we could choose to only scale up. Depending on the application, this could be a more performant option. Here we will assume that maximizing memory efficiency is a worthwhile pursuit.

(definterface IHashTable
  (calcSize [])
  (maybeResize [])
  ...
  (insert [k v resize?])
  (insert [k v])
  ...)

(deftype HashTable
    [^:volatile-mutable buckets
     ^:volatile-mutable occupancy
     ^:volatile-mutable size
     load-factor]
  IHashTable
  (calcSize [_]
    (when (-> occupancy zero? not)
      (cond
        ;; shrink
        (< occupancy (/ (* size load-factor) 2)) (/ size 2)

        ;; grow
        (> (/ occupancy size) load-factor) (* size 2))))

  (maybeResize [this]
    (when-let [new-size (.calcSize this)]
      (let [old-buckets buckets]
        ;; set size and buckets prior to re-inserting from
        ;; old-buckets
        (set! size new-size)
        (set! buckets (make-array INode new-size))

        ;; Loop over all old buckets. For any buckets containing
        ;; linked list nodes, walk these nodes. Extract their
        ;; keys and values, inserting them into the new buckets
        ;; array without triggering a call to maybeResize.
        (dotimes [i (alength old-buckets)]
          (if-let [bucket (aget old-buckets i)]
            (loop [node bucket]
              (when node
                (do (.insert this (.getKey node)
                                  (.getVal node)
                                  false)
                    (recur (.getNext node))))))))))

  ...

 (insert [this k v resize?]
    ...
    (when resize? (.maybeResize this)))

  (insert [this k v] (.insert this k v true))

  ...)

To achieve dynamic resizing, we have introduced two new methods calcSize and maybeResize which determine a new size if any and resizes when we have a new size, respectively. Additionally we now construct the hash table type with occupancy and load-factor. We need to track how many indexes actually contain linked lists. This is what we use occupancy for, incrementing it whenever we add a new bucket. Our load factor is some percentage, e.g. 7/10 or 70%.

We are also using set! to assign new values to the mutable fields on our hash table. This is important because we must ensure we update the size and occupancy as they change. In the case of occupancy we must update its value inline where we insert a node into a previously empty bucket, i.e. the third case of our cond in the insertion method.

Now we also preemptively handle a potential bug: when we call maybeResize and we find ourselves with a new size we want to reuse our insertion method so that we do not duplicate the logic used to populate the buckets array. To make this work we ensure that we hold the previous buckets in a locally bound var old-buckets and then set buckets on our hash table to a new array of the proper type and size. Now we can simply walk the nodes of old-buckets and call insert.

However, because insert makes a call to maybeResize we need to be careful that we do not trigger a resize in the midst of populating the new buckets. To avoid this, we define a new method insert that contains the relevant logic but takes a new argument resize?, a flag indicating if we should call maybeResize. This allows us to safely make the insertion calls, reusing the same code.

Okay. We should make sure this behaves as expected:

=> (def hash-table
     (let [size 1 load-factor 7/10]
       (HashTable. (make-array INode size) 0 size load-factor)))
=> (.insert hash-table "foo" "bar")
=> (.lookup hash-table "foo")
"bar"

To make hash table construction even easier we could define a simple helper:

(defn hash-table [& [size load-factor]]
  (let [size (or size 1)
        load-factor (or load-factor 7/10)]
  (HashTable. (make-array INode size) 0 size load-factor)))

This is starting to look pretty good. We have a hash table that can handle collisions and makes a decent effort to ensure runtime complexity is better than O(n) on average. There is still another step we can take to improve our current implementation.

Type Hints

One thing we have not touched on is type hints. Clojure is dynamically typed and as such you will not often find yourself worrying about types in your code. But for this to work with Java interop, for example, Clojure has to fallback to a reflection strategy, unless we tell the compiler otherwise. What this essentially means is the compiler will try to guess the correct type a given method takes. This guessing process is expensive overhead. Often it can be eliminated. Please note, this technique cannot be used to make native Clojure code faster, this is strictly an optimization around JVM interop.

The first step in evaluating reflection sensitive contexts is to set the dynamic var called *warn-on-reflection* to true:

=> (set! *warn-on-reflection* true)

With that set, the reader will warn us when it encounters calls that fallback to reflection for resolution. There are numerous points in our code where this applies, most of them relate to places where we have called our INode interface methods without informing Clojure’s compiler of the object’s type, i.e. INode.

The syntax for a type hint is a caret (^) followed by the type. So in our case we will use ^INode to indicate a var that is bound to a type that implements the INode interface. Most or all of our reflection warnings will be remedied by this notation. If we update these now we should end up with something like this:

(deftype HashTable
    [^:volatile-mutable ^objects buckets
     ^:volatile-mutable ^long occupancy
     ^:volatile-mutable size
     ^float load-factor]
  IHashTable

  (maybeResize [this]
    (when-let [new-size (.calcSize this)]
      (let [old-buckets buckets]
        ...
        (dotimes [i (alength old-buckets)]
          (if-let [bucket (aget old-buckets i)]
            (loop [^INode node bucket]
              ...))))))

  ...

  (findNode [this k]
    (when-let [bucket (.getBucket this k)]
      (loop [^INode node bucket prev nil]
        ...)))

  (insert [this k v resize?]
    (let [[^INode prev ^INode node] (.findNode this k)]
      ...))

  ...

  (lookup [this k]
    (let [[_ ^INode node] (.findNode this k)]
      ...)))

This improves performance greatly. Your mileage may vary, and you should use tools, like criterium, to verify your own results. On the machine this was implemented, insertion speed increased ~110x, compared with the non-hinted implementation.

Here is how you might use Criterium to benchmark the implementation:

=> (require '[criterium.core :refer :all])
=> (let [^IHashTable ht (hash-table)]
     (with-progress-reporting
       (bench (.insert ht (rand) (rand))))

Type hints are an important aspect of performance when implementing a custom type with deftype: otherwise reflection is often necessary. When performance is important, always make sure that reflection is eliminated wherever possible.

Conclusion

Here we looked at one method of implementing a hash table. There are numerous variations on what we have done here. But in the interest of applying our previous work with linked lists we chose to use nodes, much like the ones we implemented in the previous article, as the values of the array containing our key-value pairs. Thus our hash table consists essentially of a an array of linked lists.

We explored the nuances of handling hash collisions and ensuring that the better runtime guarantees of a hash table are met by creating a heuristic that resized our underlying array as the number of pairs in our table grew or shrank.

Our implementation made use of a hash collision resolution strategy known as separate chaining. But we could have used other techniques, such as open addressing, instead. These strategies have differing merits. The problem domain this data structure will be used in should be considered when choosing things such as collision resolution schemes.

Finally we looked briefly at type hints. Type hints are important where Java interop occurs because without them, your programs may have to resort to reflection. This can impact performance. When types are understood ahead of time via hints, this process of reflection can be eliminated.

Putting it all Together

To round off our implementation we have one final method to implement: delete. We have left it off throughout so that the code snippets are more manageable and because it should be fairly easy to see how it might be done. But in the interest of a comprehensive implementation let us finish off by adding it:

(definterface IHashTable
  (calcSize [])
  (maybeResize [])
  (bucketIdx [k])
  (getBucket [k])
  (setBucket [k v])
  (findNode [k])
  (insert [k v resize?])
  (insert [k v])
  (lookup [k])
  (delete [k]))

(deftype HashTable
    [^:volatile-mutable ^objects buckets
     ^:volatile-mutable ^long occupancy
     ^:volatile-mutable size
     ^float load-factor]
  IHashTable
  (calcSize [_]
    (when (-> occupancy zero? not)
      (cond
        ;; shrink
        (< occupancy (/ (* size load-factor) 2)) (/ size 2)
        ;; grow
        (> (/ occupancy size) load-factor) (* size 2))))

  (maybeResize [this]
    (when-let [new-size (.calcSize this)]
      (let [old-buckets buckets]
        (set! size new-size)
        (set! buckets (make-array INode new-size))

        ;; Loop over all old buckets. For any buckets containing
        ;; linked list nodes, walk these nodes. Extract their
        ;; keys and values, inserting them into the new buckets
        ;; array without triggering a call to maybeResize.
        (dotimes [i (alength old-buckets)]
          (if-let [bucket (aget old-buckets i)]
            (loop [^INode node bucket]
              (when node
                (do (.insert this (.getKey node)
                                  (.getVal node)
                                  false)
                    (recur (.getNext node))))))))))

  (bucketIdx [_ k] (mod (hash k) size))

  (getBucket [this k] (aget buckets (.bucketIdx this k)))

  (setBucket [this k v] (aset buckets (.bucketIdx this k) v))

  (findNode [this k]
    (when-let [bucket (.getBucket this k)]
      (loop [^INode node bucket prev nil]
        (if (or (nil? node) (= (.getKey node) k))
          (vector prev node)
          (recur (.getNext node) node)))))

  (insert [this k v resize?]
    (let [[^INode prev ^INode node] (.findNode this k)]
      (cond
        ;; 1. bucket contains a linked list but not our key,
        ;;    set the next node
        (and prev (nil? node)) (.setNext prev (Node. k v nil))

        ;; 2. bucket contains a linked list and our key, reset 
        ;;    value
        node (.setVal node v)

        ;; 3. bucket is empty, create a new node and set the 
        ;;    bucket
        :else (do (.setBucket this k (Node. k v nil))
                  (set! occupancy (inc occupancy)))))
    (when resize? (.maybeResize this)))

  (insert [this k v] (.insert this k v true))

  (lookup [this k]
    (let [[_ ^INode node] (.findNode this k)]
      (when node
        (.getVal node))))

  (delete [this k]
    (let [[^INode prev ^INode node] (.findNode this k)]
      (cond
        ;; 1. non-head node contains the key, update its
        ;;    neighbors
        (and prev node) (.setNext prev (.getNext node))

        ;; 2. head node contains the key, update the head
        node (.setBucket this k (.getNext node))))
    (.maybeResize this)))

Future Posts

Building upon our previous work with linked lists, we have implemented a hash table. In our next tutorial we will adapt our node class once again to take a look at trees.